|
SNAP Library 6.0, Developer Reference
2020-12-09 16:24:20
SNAP, a general purpose, high performance system for analysis and manipulation of large networks
|
|
SNAP Library 6.0, Developer Reference
2020-12-09 16:24:20
SNAP, a general purpose, high performance system for analysis and manipulation of large networks
|
#include <kronecker.h>
Public Member Functions | |
| TKronMomentsFit (const PUNGraph &G) | |
| TFltQu | EstABC (const int &R) |
Static Public Member Functions | |
| static void | Test () |
Public Attributes | |
| double | Edges |
| double | Hairpins |
| double | Tripins |
| double | Triads |
Definition at line 303 of file kronecker.h.
|
inline |
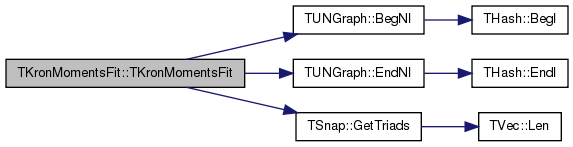
Definition at line 307 of file kronecker.h.
References TUNGraph::BegNI(), TUNGraph::EndNI(), and TSnap::GetTriads().
|
inline |
Definition at line 323 of file kronecker.h.
References TMath::IsInEps(), and TFlt::Mx.
Referenced by Test().
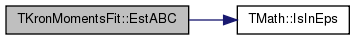

|
inlinestatic |
Definition at line 367 of file kronecker.h.
References TSnap::DelSelfEdges(), EstABC(), TKronMtx::GetKronIter(), TUNGraph::GetNodes(), TNGraph::Load(), and TSnap::PrintInfo().

| double TKronMomentsFit::Edges |
Definition at line 305 of file kronecker.h.
| double TKronMomentsFit::Hairpins |
Definition at line 305 of file kronecker.h.
| double TKronMomentsFit::Triads |
Definition at line 305 of file kronecker.h.
| double TKronMomentsFit::Tripins |
Definition at line 305 of file kronecker.h.